|
第1話の冒頭で宣言したように,材料力学は力学でした.そしてそれがどんな力学であるかは,末尾の予告でその一端を示したように「材料力学は連続体である弾性体を解析の対象にし,構造物の強度を判定する線形静力学」というものでした.
そこで,この第2話ではそれがどんな仕組みになっているのか,言い換えれば,この材料力学という物語に登場してくるキャストをご紹介しようと思います.
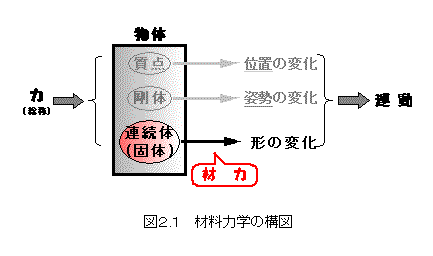
力学の概念の中で,材料力学の占める位置は図2.1のようになっていますが,以下,この構図を終始念頭におきながら,解説を進めていくことにします.
■2−1 材料力学における〈力〉と〈変形〉の諸形態
図2.1に見るように,材料力学においては,原因は当然〈力〉となりますが,結果としては〈形の変化〉を考えることになります.ここのところが,「質点の力学」や「剛体の力学」とはその趣を異にします.
そして材料力学では,一口に〈力〉とか〈形の変形〉といってもそれらの形態は原因と結果という構図で互いに関連しあって様々に分化されて扱われます.
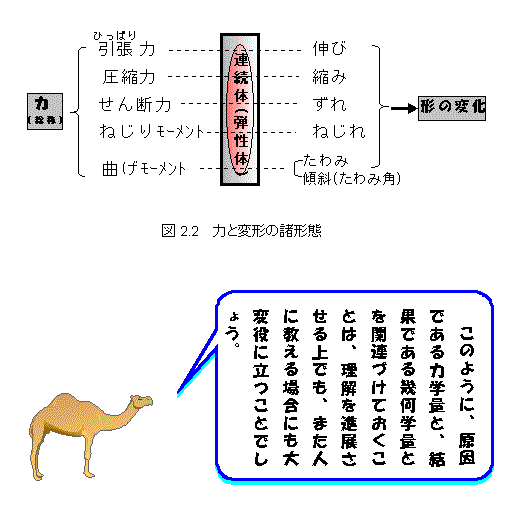
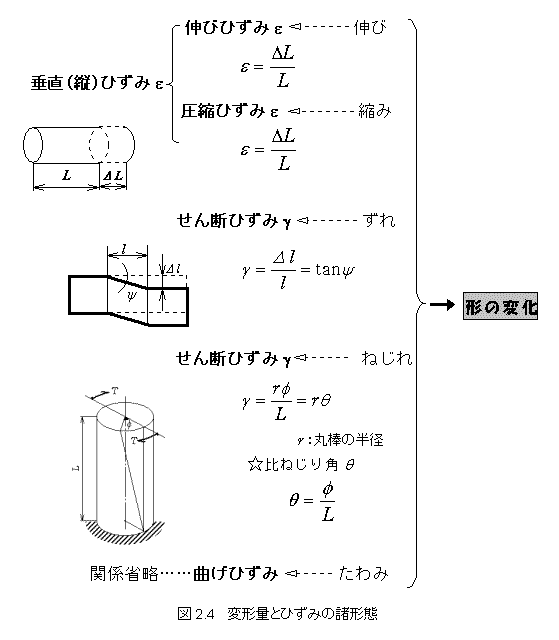
そこで,材料力学に現れる〈力〉と〈形の変化〉の諸形態を関連づけながら整理すると,次の図2.2のようになります.
■2−2 新しい力学量,〈応力〉の導入
材料力学をはじめとする連続体を扱う力学では,「質点の力学」や「剛体の力学」では全く馴染みのなかった,新たに内力(ないりょく)という考え方を導入します.これが材料力学を学ぶ上での1つのキーポイントになります.因みにこれに対する語は外力となります.要するに材力では,力学量である力を〈外力〉と〈内力〉に分けて考えるのです.
* *
さて,その外力とは文字通り物体に外部から作用する力のことですが,一方の内力の方は,物体が外力を受けるときその内部のある断面に分布している物質同士が互いに及ぼしあう力のことをいいます.この力を物質粒子一個当たりの力として考える方が理解しやすいところなのですが,実際,物質粒子がその断面にいくつあるのか,また整然と並んでいるのか,そもそも物質粒子とは厳密にどう定義すべきか等々確定するにはかなりの困難を要します.そこで物質粒子一個一個等という微視的なとらえ方をやめてもっと巨視的に捉え,粒子を面積に置き換えることにして,内力を単位面積あたりの力で表すことにするのです(こういう巨視的捉え方は“古典論”と呼ばれます.それに対するものは“量子論”).
そしてその内力を〈応力〉と呼んでいるのです.また応力度とも呼ばれますが,機械工学分野では応力ということの方が今はほとんどです.
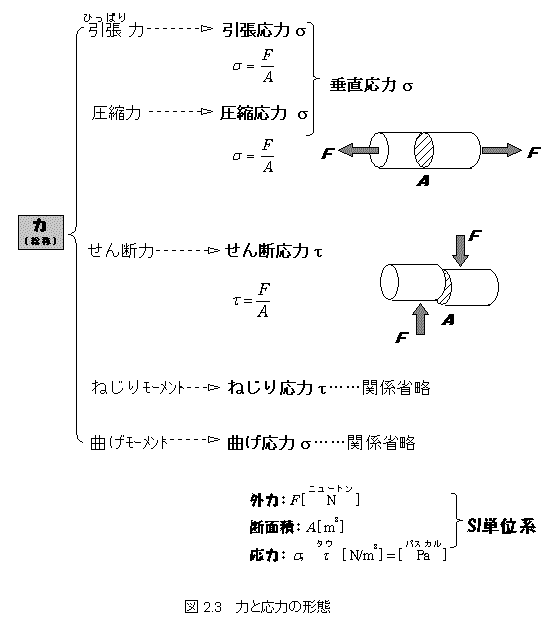
さて,そこで内力としての応力ですが,外力の諸形態にあわせてそれぞれ次のように定義されています.
引張応力と圧縮応力は符号が逆になっているだけなのでひとまとめにして垂直応力と呼んで,同じ記号で表します.
また,ねじり応力や曲げ応力の式での表現は多少複雑になりここでは割愛しますが,結局,ねじり応力とは回転形式のせん断応力に他なりませんし,曲げ応力の中身は垂直応力です.したがって,ここでは基本となる垂直応力(引張応力と圧縮応力)とせん断応力について押さえておけばひとまず十分であろうと思います.
■2−3 新たな幾何学量,〈ひずみ〉の導入
一方,幾何学量である〈形の変化〉においても,前項と同様に質点や剛体の力学にはなかった新たな幾何学量を導入します.これもやはり連続体を扱う上での特質といえるのです.
材料力学では長さや角度といった量をそのまま用いないで,それをある種の比率すなわち変形率に表すことを考えます.それがすなわち〈ひずみ〉というわけです.これも力を外力と内力に分けて考えたように,ひずみもまた目に見える幾何学量でない物質内部での内的な量として捉えることができます.
ひずみも応力と同様に,変形の諸形態に対応してそれぞれ次のように定義されています.
ひずみは長さの比になっているので,単位は1の無次元数です.
伸びひずみと圧縮ひずみは符号が逆になっているだけなのでひとまとめにして垂直または縦ひずみと呼んで,同じ記号で表します.一方,ねじれに関しては回転形式のせん断ひずみであり,本質的にずれと変わりありませんが,ただ新たに〈比ねじり角〉というものが登場して来ることに注意しておいて下さい.また,たわみに対しては曲げひずみというものが定義されますが,その中身は垂直ひずみに他なりません.
したがって,ここでは基本となる垂直ひずみ(伸びひずみと圧縮ひずみ)とせん断ひずみについて押さえておけばひとまず十分です.ただ,比ねじり角というものがあることをお忘れないように…….
予告編 二つの世界をつなぐもの
さて,運動の原因となる〈力〉は力学の世界の量である.一方,結果となる〈変形〉は幾何学の世界の量である.考えてみれば,この二つの世界は全く異質の世界であり,何ら必然的な関係が保証されているわけではない.その異質な二つの世界に橋渡しをした偉大な法則がある.もしこれがなかったならば「変形の力学」の発展は望むべくもかったであろう.
次回は,その偉大なる法則の材料力学における活躍ぶりをご紹介しましょう.
|