|
前話では,〈力〉が原因となって,その結果として〈変形〉が起こるという構図で話を展開してきました.もちろん,それを適用する対象は〈物体〉でした.
ところで,その〈力〉という量は文字通り力学量ですし,一方,結果となる〈変形〉は長さの変化や角度の変化でしたから,これは幾何学量以外の何者でもないでしょう.それにしても,このことを改めてじっと考えてみると,なぜこの異質な量が必然的関係にあるかのように理解してしまっているのか,疑問を覚えてないでもありません.それをカント流に言えば,体験に基づいた総合判断として暗黙の内に了解されていたというところでしょう.しかしそのような関係について誰かが明確な形式を提言しなければ,科学的な意味でのこの因果関係の成立はなかったと見るべきでしょう.
そこでこの第3話では,この力学量と幾何学量という異質な二つの世界の橋渡しをした,その偉大なる法則についてご紹介したいと思います.
■3-1 〈力学量〉と〈幾何学量〉をつなぐ式
本題に入る前に,ここでは,先ずここまでの物語に出てきた各種の力学量と各種の幾何学量の対応関係を整理しておきましょう.
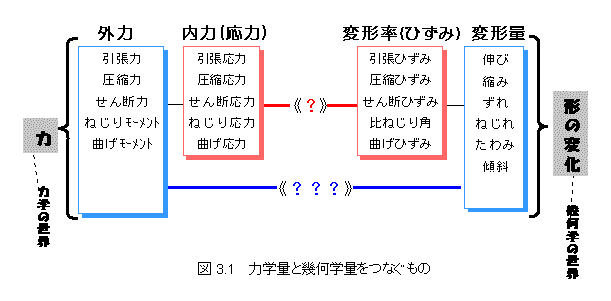
変形を考える材料力学では,力を〈外力〉と〈内力(応力)〉とに分けました.一方,変形は例えば〈伸び量〉と〈伸び率(ひずみ)〉に分けて考えました.そして,それらの対応の仕方はちょうど図3.1のようになっています.
この図から分かるように,〈応力〉―〈ひずみ〉で一つの対応関係が,〈力〉―〈変形量〉でまた一つの対応関係があることが分かります.つまり,内側同士,外側同士で考えればよいというわけです.
さて上図において,《?》や《???》の中にどんな関係式が入るかが,これからの話題になります.
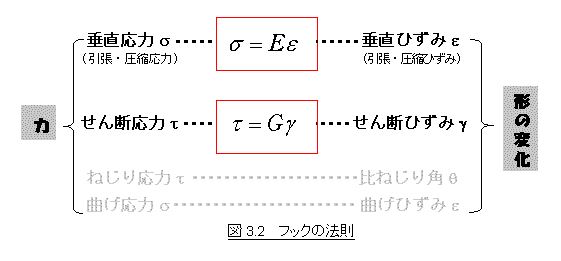
(1)〈応力〉と〈ひずみ〉をつなぐもの――フックの法則
力学的な量である〈応力〉と幾何学的な量である〈ひずみ〉という異質な二つの量を関係づけている唯一ものが,実は〈フックの法則〉と呼ばれるものなのです.〈フックの法則〉は普段はバネの伸びと力の関係として何気なく耳にしているものですが,実はまったく異なる概念からなる二つの世界をしっかり橋渡しするという役割を担った偉大な法則だったのです.
さて,そのフックの法則は〈応力〉と〈ひずみ〉の形態に応じて次のように定義されています.
ここに,比例定数Eは縦弾性係数あるいはヤング率といわれ,また,Gは横弾性係数(せん断弾性係数)と呼ばれます.詳細は後ほど説明することに致しましょう.
なお,ねじりや曲げについては本質的にそれぞれ垂直応力とせん断応力の場合と変わらないので,その場合の具体的な形は割愛することにします.
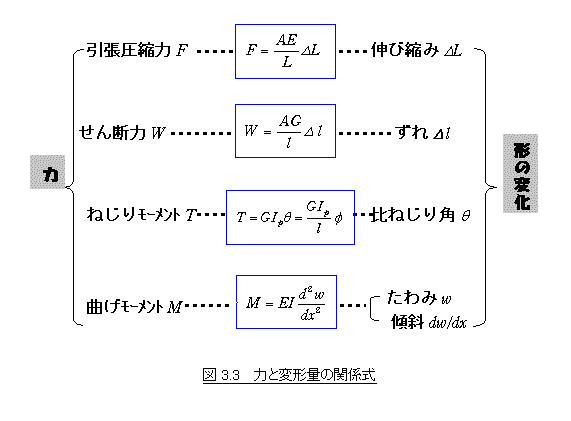
(2)〈力〉と〈変形量〉をつなぐ式――これもフックの法則
〈外力〉と〈変形量〉との関係は前節(1)の結果から自動的に次のように表されます.なお,ねじりや曲げを考える際には真っ直ぐな棒(断面幅に対して長さが十分長い部材)に限定してその関係式を示しています.
ここに,Aは断面積,Ipは断面2次極モーメント,Iは断面2次モーメントで,何れも断面に関する幾何学的特性値です.その詳細はまた後ほど説明致します.
また,次のような量もしばしば登場してきます.頭の隅にでも…….
AE:伸び剛性……伸びにくさを表す
AG:せん断剛性……せん断のしにくさを表す
GIp:ねじり剛性……ねじりにくさを表す
EI:曲げ剛性……曲げにくさを表す
特にこれらの関係式そのものに対し〈フックの法則〉という呼び方は余りしませんが,意味の上からは,〈フックの法則〉に他なりません.特に,上図最上段にある引張・圧縮力と伸縮量の関係は,係数AE/Lをバネ定数kと考えれば,まさにバネの伸びと力の関係を表すフックの法則そのものです.
■3-2 材料力学における特性値一覧
変形の力学では,いま見たようにヤング率であるとか断面2次モーメントであるとか,とにかくいろいろな特性値が表れてきます.以下にそれらを一斉に説明してみます.
(1)物質的特性値(物性値)/力学の世界に属する
①密度
物質の単位体積当たりの質量をいいます(物質1m3は何㎏かという値).これは物質ごとに固有の値を持ち,物性値です.なお,熱や流体の力学ではよく〈比体積〉というものが使われますが,それはこの密度の逆数になっています(1㎏の質量が占める体積).
ただ,材料力学は静力学なので,密度は直接的に使われることはありません.
②縦弾性係数と横弾性係数
『フックの法則』の中に現れる縦弾性係数Eや横弾性係数Gは材料の変形しにくさを表していて(値が大きい材料ほどひずみにくい),材料ごとに固有の値をもつ物性値です.
また,縦弾性係数と横弾性係数の間には次のような関係があります.
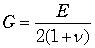 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-1) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-1)
ここに,n はポアソン比というものですが,それでは直ちに事項へ進みましょう.
③ポアソン比
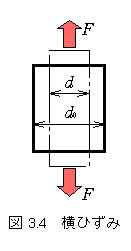
例えば丸棒を引っ張るとき,丸棒の直径は減少します.反対に圧縮すれば増加します.つまり,垂直応力の生じる方向と直角な方向にもひずみを定義できるということで,このひずみのことを〈横ひずみ〉といいます.
右図において〈横ひずみ〉はもとの直径に対する直径の減少率で次のように表すことができます.
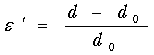 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3-2) ・・・・・・・・・・・・・・・・・・・・・・・・・・(3-2)
さてこのとき,弾性限度内ででは縦ひずみ(垂直ひずみ)eと横ひずみe’は比例関係にあることが知られていて,そのときの比率をポアソン比とかポアソン数と呼んでいいます.その定義はそれぞれ次の通りです.
ポアソン比n
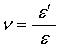 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-3) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-3)
ポアソン数m
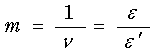 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-4) ・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-4)
ここまでの密度,弾性係数,ポアソン比は実際どんな値かを表3.1で確認することにしましょう.
表3.1 材料の物性値
材 料
|
縦弾性係数
E [GPa] |
横弾性係数
G [GPa] |
ポアソン比
n |
密 度
r [kg/m3] |
鋼
炭素鋼・合金鋼
鋳 鉄
黄 銅
アルミ合金
ガ ラ ス
コンクリート
|
206
206
98
103
73
69
20
|
80
80
34
41
26
|
0.3
0.3
0.3
0.33
0.33
0.22
0.2
|
×103
7.86
7.86
7.86
8.65
2.7
2.5
2 |
(日本機械学会編『機械実用便覧』(丸善刊1990)に基づいて表を構成)
④体積弾性率
弾性率としては縦と横の他に体積変化のしにくさを表す,体積弾性係数Kというものがあります.固体ではあまり問題になりませんが,液体や気体などを扱う上では大変重要な弾性率です.
体積弾性率は縦弾性係数と一意な関係があり次の通りです.
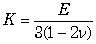 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-5) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-5)
また,体積変化の際には,内力としては〈圧力p〉を,変形率としては〈体積ひずみev〉を考え,それらの間にやはり次のフックの法則が成り立ちます.
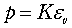 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-6) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-6)
ここに,体積ひずみは次の通りです.
 ・・・・(3-7) ・・・・(3-7)
因みに,体積弾性率Kの逆数は圧縮率と呼ばれます.
(2) 幾何学的特性値/幾何学の世界に属する
棒に関しての諸特性を整理します.
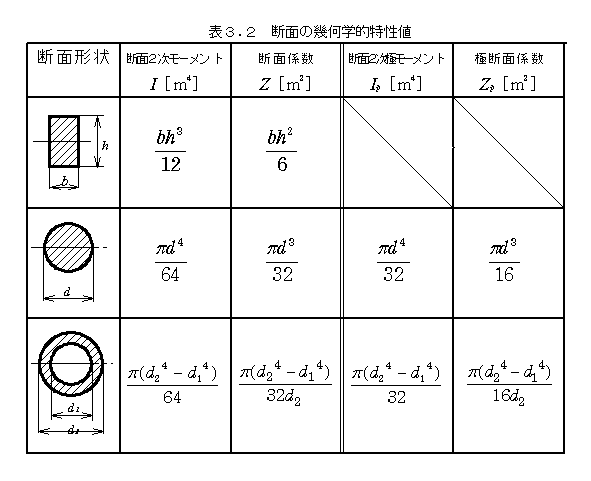
①断面2次モーメント
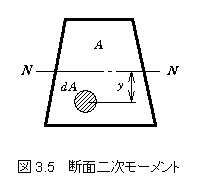 断面を無数の微小断面積dAに分割し,その各々について,ある回転軸からの距離の2乗y2を掛けてそれらを全て足し合わせて計算されるもので,長さの4乗の次元を持ちます. 断面を無数の微小断面積dAに分割し,その各々について,ある回転軸からの距離の2乗y2を掛けてそれらを全て足し合わせて計算されるもので,長さの4乗の次元を持ちます.
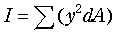 ・・・・・・(3-8) ・・・・・・(3-8)
回転軸とは,棒が曲がるときその断面はわずかに回転するわけですが,その時の中心軸を意味します(右図ではN-Nです).この断面2次モーメントは曲げに関して,幾何学的意味で(図形の上で)の変形しにくさを表しています.
因みに,ヤング率などは力学的な意味での変形のしにくさを表しています.
②断面2次極モーメント
これはねじりに関する断面2次モーメントで,幾何学的なねじりにくさを表します.分割した微小断面dAと同一面内にある1点との距離の2乗r2を掛けて足し合わせて計算します.
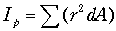 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-9) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-9)
③断面係数
断面係数ははりの曲げ問題の中で出てくるもので,断面2次モーメントをはり断面の中立軸とはり表面までの距離Hで割って得られ,長さの3乗の次元を持ちます.曲げ応力(後述します,実は垂直応力に他ならない)の計算に用いられます.
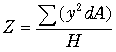 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-10) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-10)
④極断面係数
極断面係数は丸棒のねじり問題の中で出てくるもので,丸棒について定義され,断面2次極モーメントを棒の半径Rで割って得られ,長さの3乗の次元をもちます.ねじり応力の計算に用いられます.
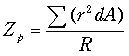 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-11) ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-11)
以上の幾何学的特性値を総括すると次の表のようになります.なお,上式の表現では総和記号Σで計算の仕方を表しましたが,実際は積分によって計算しています.
予告編 引張りとせん断を科学する
さて,3話にわたって材料力学の基礎的な理解を深めることに主眼をおいて話を進めてきたが,次回から,いよいよ具体的な,“使える材力”に視点を移して話題を提供していく.
次回では,まず基本的な「引張りとせん断」について話を展開しよう.
| 




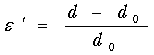 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3-2)
・・・・・・・・・・・・・・・・・・・・・・・・・・(3-2)
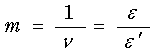 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-4)
 ・・・・(3-7)
・・・・(3-7)
 断面を無数の微小断面積dAに分割し,その各々について,ある回転軸からの距離の2乗y2を掛けてそれらを全て足し合わせて計算されるもので,長さの4乗の次元を持ちます.
断面を無数の微小断面積dAに分割し,その各々について,ある回転軸からの距離の2乗y2を掛けてそれらを全て足し合わせて計算されるもので,長さの4乗の次元を持ちます.
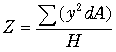 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-10)
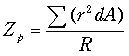 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3-11)